KI-Entwicklung: Mein Weg zum Perzeptron

Ein Computer, der denkt wie ein Mensch – eine künstliche Intelligenz? Wie funktioniert das?

Dieser Frage ein Stück weit auf den Grund zu gehen, ist die Ambition hinter einem Selbstversuch, an dessen Ende die Entwicklung eines sehr einfachen neuronalen Netzes stehen wird. Damit willkommen zum zweiten Teil unserer gemeinsamen Reise zum Perzeptron, welche in meinem Artikel in der sechsten Ausgabe des Magazins gråd extra ihren Anfang nahm.

Was bisher geschah

Ziel dieses Selbstversuchs sollte es sein, die einfachste Form eines neuronalen Netzes zu entwickeln, ein einzelnes Perzeptron.

Dieses Perzeptron sollte in der Lage sein, lineare Probleme zu lösen. Konkret ging es um die Zuordnung von zufälligen Punkten in einem kartesischen Koordinatensystem, als oberhalb oder unterhalb einer Linie, deren Verlauf durch eine Funktion von x definiert wurde. Bisher haben wir kennen gelernt:

1. Dateneingänge: Wir übermitteln dem Perzeptron die Koordinaten (x,y) eines beliebigen Punktes
2. Summenfunktion: Die Koordinaten werden addiert
   summe = x + y
3. Aktivierungsfunktion: Ist das Ergebnis der Summenfunktion größer gleich null, nimmt das Perzeptron an, das der gegebene Punkt oberhalb der Linie liegt – wir nennen dieses Vorgehen Binary Step
   oberhalb = x + y >= 0
4. Weights: Damit das Perzeptron variabel auf unterschiedliche Linienfunktionen reagieren kann, ergänzen wir Weights als Faktoren in die Summenfunktion
   oberhalb = (x * Wx) + (y * Wy) >= 0

Lineare Regression

Um 19 Uhr scheint die Sonne! Einen wolkenfreien Himmel vorausgesetzt ist dies eine Wahrheit, die wir lernen, wenn wir im Sommer um 19 Uhr aus dem Fenster sehen. Schauen wir hingegen im Winter aus dem Fenster, wird diese Wahrheit schnell an der Realität scheitern – denn die Sonne ist längst untergegangen.

Als Mensch suchen wir nach den entsprechenden Einflussfaktoren, von welchen es neben der Uhrzeit abhängt, ob die Sonne scheint oder nicht. Wir nehmen Stichproben, die wir Erfahrungen nennen:

• im Sommer um 19 Uhr ja
• im Winter um 19 Uhr nein
• im April um 17 Uhr ja

Erfahrungslücken gleichen wir dabei mit Schätzungen aus. In der Statistik wird dieses Vorgehen Regressionsanalyse genannt und ein Spezialfall, die lineare Regression, wird interessant, sobald man sich mit dem Lernprozess einer künstlichen Intelligenz beschäftigt.

Versuch und Irrtum

Kehren wir zurück zu unserer angepassten Summenfunktion:
oberhalb = (x * -1) + (y * -1) >= 0
Anstatt von Monaten und Uhrzeiten, sprechen wir hier nur noch ganz abstrakt von x und y. Unser bisheriger Punkt welcher oberhalb unserer Linie liegen soll, war bei (2, -5) definiert. Schauen wir uns diesen Fall grafisch in einem Koordinatensystem an, können wir feststellen, dass es unendlich viele Linienfunktionen gibt, für welche dies zutrifft.

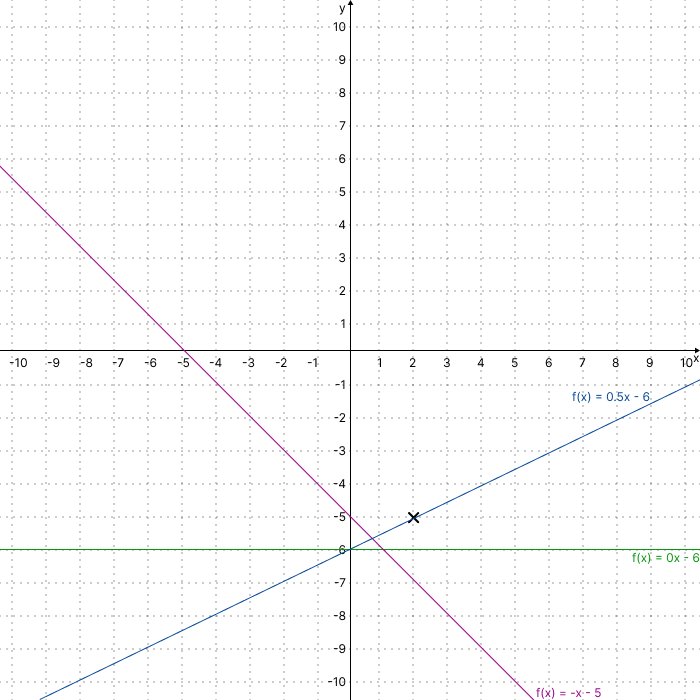
Um die Auswahl weiter zu schärfen, benötigt das Perzeptron weitere Beispielpunkte, welche jeweils mit der Aussage markiert sind, ob diese oberhalb der Linie liegen oder nicht. Das Perzeptron nimmt diese Punkte entgegen und stellt zunächst eine eigene Vermutung an. Danach wird diese Vermutung mit unserer Aussage verglichen. Stimmen Vermutung und Aussage überein, passiert nichts weiter. Stellt das Perzeptron jedoch eine Abweichung fest, muss gehandelt werden.

Die Fehlerberechnung

Ziel des Lernprozesses unserer kleinen KI ist es, den minimalen Fehler unserer Summenfunktion zu ermitteln. Der erste wichtige Zwischenschritt dabei sieht vor, die Abweichung zwischen unserer Aussage und der Vermutung des Perzeptrons zu berechnen. Generell können wir diese Abweichung als Differenz zwischen Aussage und Vermutung berechnen, also mit der Formel:
Abweichung = Aussage - Vermutung

In diesem Moment können wir mit ausgeprägtem Frohgemut auf die recht früh getroffene Entscheidung der Wahl einer Binary Step Funktion als Aktivierungsformel zurückblicken. So beschränkt sich die Menge potenzieller Vermutungen und Aussagen auf die Werte -1 und 1. Oder in unserem speziellen Fall: unterhalb der Linie, oberhalb der Linie.

Stellt man nun die möglichen Vermutungen des Perzeptrons und unsere potenziellen Aussagen tabellarisch gegenüber, entsteht diese überschaubare Matrix.

Aussage	Vermutung	Abweichung
-1	1	-2
-1	-1	0
1	1	0
1	-1	2

Ende Tag 3 – der Endspurt naht. Zeit für einige Seitenbetrachtungen. Wer schon einmal Vogel- oder Fischschwärme beobachtet hat, muss das harmonische Zusammenspiel bemerkt haben. Ohne dass es ein konkretes Leittier zu geben scheint, schafft es der Schwarm sich zusammenhängend in eine gemeinsame Richtung zu bewegen. Richtungsänderungen werden dabei von allen Tieren übernommen.

Im Jahr 1986 wurde vom KI-Experten Craig W. Reynolds eine Simulation geschaffen, welche auch jenes Schwarmverhalten nachstellt. Grundlage dieser Simulation sind 3 Formeln welche das Verhalten jedes einzelnen Tieres im Schwarm berechnen. Und eine dieser Formeln, genauer gesagt der „Seeking Steering Algorithm“, kann verwendet werden, um Fehler in den Weights eines Perzeptrons auszugleichen.
(Wer Interesse hat kann unter https://www.infomax-online.de/ftp/boids/ eine derartige Simulation selber ausprobieren)

Fehlerkorrektur

Stellt das Perzeptron einen Fehler fest, so erscheint es erst einmal naheliegend, die Weights direkt so anzupassen, dass für die gegebenen Koordinaten das erwartete Ergebnis erzielt wird. Wir sind jedoch nicht auf der Suche nach einer Summenfunktion, welche für jedes vorgegebene Koordinatenpaar unabhängig von allen anderen Koordinaten jeweils die erwartete Aussage trifft. Wie bei einem Vogelschwarm sind wir auf der Suche nach dem gemeinsamen Mittelwert, welcher für alle gegebenen Koordinatensätze den insgesamt minimalst möglichen Fehler liefert, so dass am Ende alle in die gleiche Richtung fliegen.

Zu diesem Zweck berechnet der „Seeking Steering Algorithm“ die Weights in einem Perzeptron nicht komplett neu, sondern optimiert die bestehenden Werte auf Grundlage der von uns ermittelten Abweichung. Eine Frage die sich bei der Korrektur unserer Weights jedoch stellt, ist die Frage nach der Schuld. Unser Perzeptron verfügt über zwei Dateneingänge, also x und y. Beide zusammen haben nun eine fehlerhafte Vermutung geliefert, aber wer von beiden ist der Übeltäter? Wir können davon ausgehen, dass in gewissem Umfang beide zu einem Teil verantwortlich sind. Tatsächlich geht der „Steering Seeking Algorithm“ davon aus, dass der Grad der Schuld direkt mit der Höhe des Input Wertes korreliert. Wir berechnen demnach einen Differenzwert Delta für unsere Weights nach der Formel
Delta Weight = Abweichung * Input
Diese Differenz wird auf den bisherigen Weight Wert addiert:
Weight = Weight + Delta Weight

Beispielrechnung:

Schauen wir einmal etwas genauer hin, wie der Algorithmus rechnet. Wir gehen von den bisherigen Weights für x und y von jeweils -1 aus.

Koordinatenset	Aussage	Vermutung	Abweichung
2, -5	1	1	0
-1, -5	1	-1	2

Unsere allgemeine Formel für die Deltas:
Delta Weight = Abweichung * Weight
Mit den konkreten Koordinaten für unseren zweiten Punkt bei -1, -5 sieht die Rechnung wie folgt aus:
Delta Wx = 2 * -1 = -3
Delta Wy = 2 * -5 = -11

Die allgemeine Formel zur Korrektur der Weights:
Weight = Weight + Delta Weight
Mit den konkreten Deltas die wir im vorherigen Schritt berechnet haben, kommen wir auf folgende Ergebnisse:
Wx(neu) = -1 + -3 = -4
Wy(neu) = -1 + -11 = -12

Die Lernrate

Nach unserer Beispielrechnung korrigiert das Perzeptron seine Weights auf die Werte -4 und -12. Eine entsprechend angepasste Summenfunktion kommt nun tatsächlich auf die korrekten Annahmen. Allerdings fällt die Anpassung der Weights bislang sehr massiv auf. Würden wir weitere Werte durchrechnen, so könnten wir feststellen, dass der Algorithmus um einen Mittelwert „drum herumtanzt“, ohne ihn tatsächlich zu erreichen – Feinabstimmungen der Weights sind so noch nicht möglich.

Ein letzter Faktor der korrigierend in die Berechnung der Delta Weights eingreift, ist die Lernrate. Diese wird mit den Delta Weights multipliziert, bevor diese auf die bisherigen Weights addiert werden. So lässt sich steuern wie stark der Einfluss des „Seeking Steering Algorithm“ auf die Weights ist. Eine niedrige Lernrate bedeutet von daher das unser Perzeptron relativ lange benötigt um die Summenfunktion des minimalen Fehlers zu ermitteln. Eine hohe Lernrate liefert schneller Ergebnisse, die jedoch relativ ungenau sind. In der Praxis wird von daher auch eine variable Lernrate verwendet. Zu Anfang des Lernprozesses sehr hoch für eine schnelle Groborientierung, danach für die Feinjustierung sehr klein. Der angepasste „Seeking Steering Algorithm“ sieht demnach so aus:
Weight = Weight + Delta Weight * Lernrate

Epilog

Und das wars – Jubel – das Perzeptron ist fertig und rechnet zuverlässig. Unter https://www.infomax-online.de/ftp/perzeptron/ kann man nun hoffentlich ein bisschen besser nachvollziehen wie eine KI funktioniert. Ein einzelnes Perzeptron ist zwar in Komplexität und Fähigkeiten sehr begrenzt und nicht mit einem vollständigen Neuronalen Netz vergleichbar. Die Grundkonzepte bleiben darüber hinaus dennoch weitestgehend die gleichen.